Salah satu bangun ruang yang banyak dijumpai adalah tabung. Bangunan ini memiliki luas, keliling dan volume dengan rumus tabung khusus dan berbeda dengan bangun ruang lainnya. Pembelajaran tentang tabung, akan sangat dibutuhkan bukan saja saat di sekolah namun di dunia kerja bahkan kehidupan sehari-hari.
Berikut ini, semua penjelasan tentang tabung akan menambah wawasan Anda. Pastinya tidak membosankan karena merupakan pelajaran menyenangkan, apalagi sangat berkaitan dengan benda yang sering digunakan atau dilihat.
Tabung Adalah
Informasi awal yang perlu dipahami adalah pengertian tabung, yaitu salah satu bangun ruang dengan tiga sisi, dua rusuk dan bagian sisi melengkung.
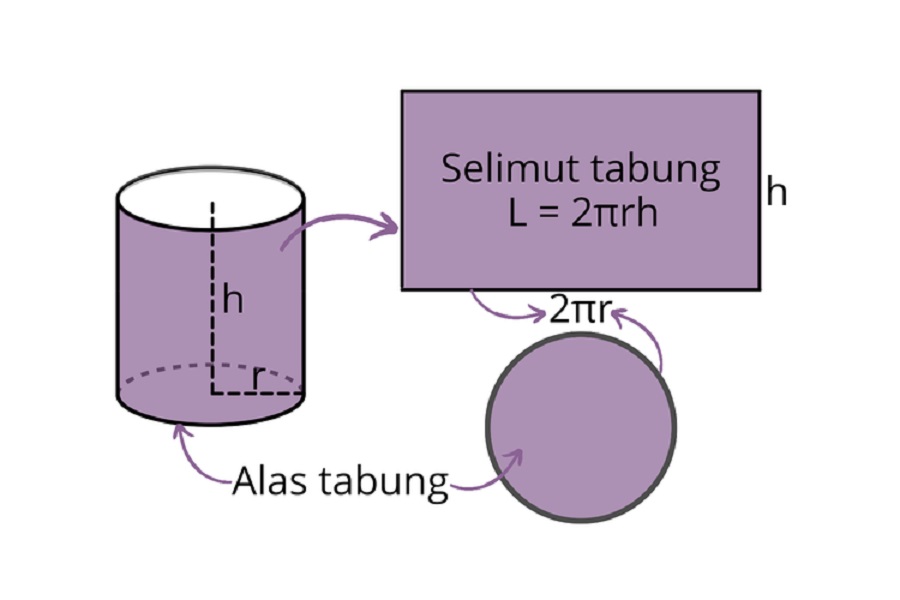
Sisi tabung, terletak pada bagian atasnya yang dikenal dengan istilah tutup tabung. Kemudian pada bagian lengkungan badannya disebut selimut tabung, dan bagian alas tabung. Sedangkan rusuknya terdapat di bagian sisi kiri dan kanan selimut atau bagian yang lengkung.
Salah satu ciri khas dari tabung adalah, bagian atasnya berbentuk bidang datar yang menyerupai lingkaran. Dimana ukuran tutupnya tersebut akan sangat membantu saat akan mencari volume maupun luas dari bangunan itu sendiri.
Kalau membahas pengertiannya secara bahasa, tabung disebut sebagai salah satu wadah yang sering dipakai untuk menyimpan barang atau bahan apapun. Berbagai jenis benda sehari-hari, bentuknya seperti tabung. Seperti botol minum, gelas, toples dan lainnya. hanya saja ukuran dan volumenya berbeda-beda.
Unsur Unsur Tabung

Untuk membedakannya dengan bangun ruang lainnya, terdapat unsur yang hanya ada pada tabung. Masing-masing memiliki nama dan karakteristik tersendiri.
Tinggi Tabung
Biasa juga disebut dengan sumbu silinder, yang merupakan garis tegak lurus pada bidang lingkaran tabung.
Jari-jari Tabung
Yaitu sebuah jarak yang diambil dari titik pusat lingkaran atas atau alas tabung menuju bagian luar lingkaran.
Diameter Tabung
Merupakan garis lurus yang diambil dari ujung sisi alas atau tutup tabung, dengan simbol D. Ukuran ini akan sangat penting dan digunakan dalam berbagai rumus tabung.
Pusat Lingkaran Tabung
Yaitu titik pada bagian tengah lingkaran pada tabung. Dihitung dari titik tengah atas atau alas. Jika ditarik jarak pada pusat lingkaran ke titik lainnya yang terletak pada kelilingnya, akan memiliki ukuran yang sama.
Selimut Tabung
Bagian selimut ini membentuk segiempat lengkung yang akan mengikuti bentuk dari sisi luar tutup dan alas bangun.
Sisi tabung
Seperti sudah dijelaskan sebelumnya, sisi tabung terdapat tiga. Dua berbentuk datar dan menyerupaki lingkaran, terletak di atas dan alas bangun tersebut. Satu lagi adalah sisi selimut tabung yang menutupi ruang antara alas dan tutup.
Ciri-ciri Tabung
Selain unsur yang dimiliki oleh bangun ruang ini, ada juga ciri pembedanya dengan bangun ruang lainnya. Apa sajakah itu?
Tidak Punya Titik Sudut
Berbeda dengan bangun ruang seperti kubus, balok dan prisma yang punya titik sudut. Tabung tidak punya karena dirangkai dari bangunan berbentuk lingkaran dan persegi panjang melengkung sebagai bagian badan atau selimut tabung.
Ada Jari-Jari
Bangunan ini memiliki jari-jari karena alas dan tutupnya terbentuk dari lingkaran. Jari-jari ini sangat penting diketahui nilainya, nantinya nilai tersebut akan dibutuhkan untuk mengetahui ukuran volume dan luas permukaan tabung.
Ada Selimut Tabung
Selimut tabung ini memiliki bentuk utama persegi panjang, kemudian akan menutup bagian diantara alas dan tutup membentuk lengkungan.
Ada Tinggi
Bangunan ini memiliki tinggi, yang diukur dari bagian alas menutup bagian tutup atasnya
Ada Rusuk
Rusuk tabung terdiri dari dua bagian, yang letaknya ada pada sisi selimut tabung
Ada Alas
Alas tabung membentuk lingkaran dan sangat menentukan volume dari sebuah tabung
Rumus Tabung
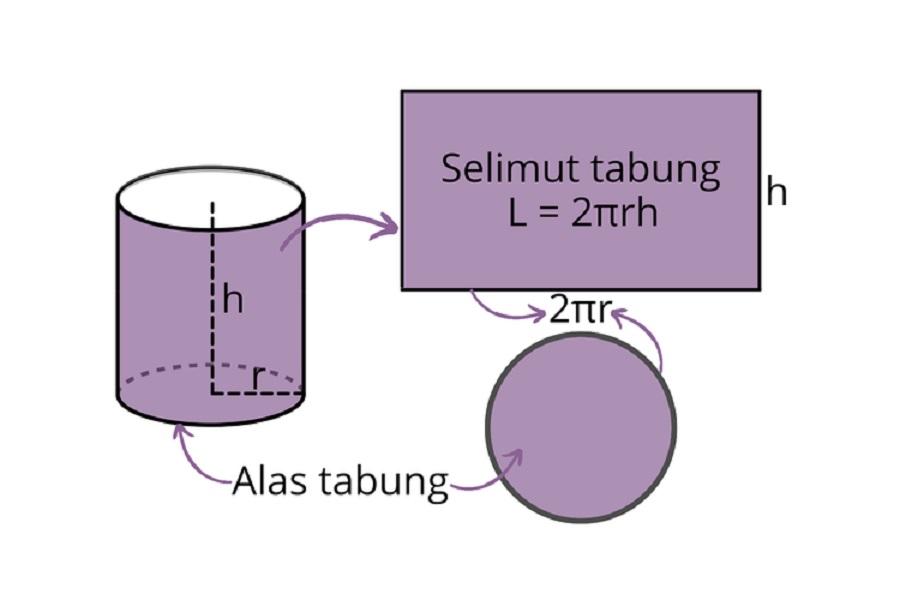
Ada beberapa rumus tabung yang penting untuk diketahui. Masing-masing rumus memanfaatkan ukuran yang ada pada sebuah tabung.
Rumus Luas Permukaan
Rumus ini akan membutuhkan jumlah luas permukaan selimut tabung dan alas serta tutup tabung. Dimana persamaan rumusnya adalah:
2πrt (r+t)
Π :koefisien yang dipakai untuk mencari nilai jari-jari dan diameter lingkaran dengan nilai 3.14
r : jari-jari tabung
t : tinggi tabung
luas permukaan tabung juga membutuhkan luas selimut tabung yang menggunakan rumus 2πrt
Rumus Volume Tabung
Beda dengan luas permukaan, untuk mencari volume sebuah tabung dibutuhkan beberapa ukuran penting daru sebuah tabung. Rumusnya adalah:
V = Π x r2t
Penjelasannya adalah:
V = volume tabung dengan satuan m3
r = jari-jari tabung
t = tinggi tabung
Π = koefisien phi yang nilainya 3.14
Rumus Luas Alas
Berhubung alas dari sebuah tabung bentuknya adalah lingkaran, maka untuk luas alas tabung menggunakan rumus luas lingkaran yaitu: Πr2
Rumus Luas Selimut
Sedangkan untuk luas selimut tabung menggunakan rumus: Πdt
Contoh Soal Tabung
Untuk lebih paham tentang berbagai rumus tabung lengkap di atas, berikut ini beberapa contoh soalnya. Bisa dijadikan referensi memahami semua bagian tabung secara lebih baik.
1. Sebuah tabung memiliki jari-jari 10 cm, sedangkan tingginya adalah 15. Berapa volume dari tabung tersebut?
Diketahui:
r=10 cm
t=15 cm
Ditanya, V?
Jawab: V= Π x r2t
V= 3,14 x 102x 15
V= 4.710 m3
d=16 cm, r=16/2 = 8 cm
t=21 cm
ditanya, luas permukaan?
Jawab:
Luas permukaan = 2πrt (r+t)
= 2 x 3,14 x 8 (8+21)
Jadi volume dari tabung tersebut mencapai 4.710 meter kubik
2. Diameter sebuah tabung adalah 16 cm, sedangkan tingginya mencapai 21 cm. Berapakah luas permukaan dari tabung tersebut?
Diketahui:
d=16 cm, r=16/2 = 8 cm
t=21 cm
ditanya, luas permukaan?
Jawab:
Luas permukaan = 2πrt (r+t)
= 2 x 3,14 x 8 (8+21)
= 1456,96 cm2
Manfaat Bangun Ruang Tabung

Pemanfaatan bangun ruang jenis tabung sangat banyak dipakai di dalam kehidupan sehari-hari maupun berbagai jenis industri. Bangun ruang ini banyak membantu berbagai aktivitas yang dilakukan secara personal maupun banyak orang.
Di Kehidupan Sehari-hari
Banyak benda berbentuk tabung yang dipakai untuk kebutuhan sehari-hari. mulai dari tabung air yang memiliki manfaat menyimpan air minum, agar bisa dibawa kemana-mana lalu diminum kapanpun Anda haus.
Kemudian celengan yang berfungsi untuk menyimpan uang yang disisihkan sebagai tabungan. Kebanyakan celengan berbentuk tabung bisa memuat lebih banyak uang kertas maupun uang logam.
Dunia Medis
Tabung oksigen di dunia medis sangat penting, membantu pasien dengan masalah pernafasan untuk bisa tetap bernafas dengan lancar. Pada tabung tersebut akan dialirkan oksigen melalui slang khusus ke bagian hidung pasien sesak nafas.
Dunia Industri Konstruksi
Untuk membuat adukan semen yang pas dibutuhkan tabung molen yang akan berputar mencampurkan semua bahan semen dalam jumlah besar. sehingga memudahkan pekerja menggunakan beton siap pakai tanpa harus mengaduknya secara manual.
Dunia Industri Pertambangan
Ada berbagai jenis tabung yang dipakai untuk ujicoba bahan tambang, untuk menentukan kualitas bahan apakah layak digunakan atau tidak.
Pelajari lebih banyak bangun ruang, akan membuat wawasan tentang berbagai jenis bangun menjadi bertambah. Seperti dari penjelasan di atas, Anda jadi tahu berbagai rumus tabung hingga pemanfaatannya di dalam kehidupan.